Data Collection Strategies Revisited

To follow up on my post earlier today on two approaches to linear model fitting, I decided to do some Monte Carlo simulations to test the relative strength of my two proposals for data collection strategies. To test the merits of sampling clustered data points versus sampling scattered data points, I generated 100,000 data sets of four sizes (N = 10, N = 100, N = 1,000, N = 10,000) using each of these two approaches. For clustered data sets, I calculated the slope of the regression line using the slope formula everyone learns from remedial algebra; for the scattered data sets, I calculated the regression coefficients using standard linear model algorithms. I then compared these slopes with the true value and calculated the absolute error for each approach. Using these individual errors, I calculated the mean absolute error for each approach. The results are plotted in the graph below and the code I used to run the simulations is at the end of this post.

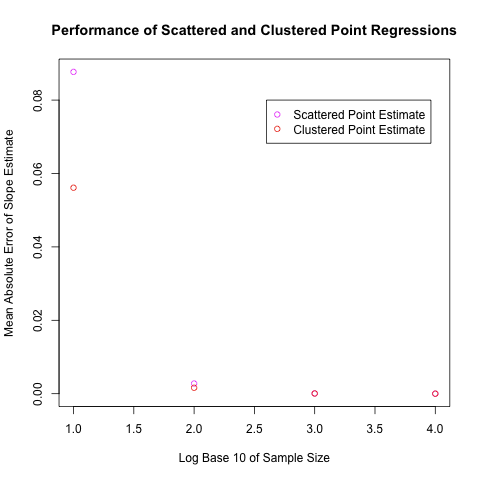
As you can see from this graph, the two approaches seem to have indistinguishable performance for large data sets, but the clustered data set approach seems to perform slightly better for data sets of size N = 10. I was quite surprised by this, as I assumed my slightly ad hoc approach would perform worse than the standard approach. I therefore would appreciate any/all of the following: theoretical analyses of the two approaches' merits for small data sets, the discovery of errors in my code, or an insight about the R function rnorm() that implies these results regardless of the intrinsic quality of the two approaches. One other conceivable source of error in these results – which I had hoped would wish out with the large number of iterations in my simulations – is that the data sets used to perform the analysis were simply incomparable, which is problematic because I compared classical regression on scattered point data sets to slope estimation on clustered point data sets. As a follow up, I should probably consider the performance of classical regression on clustered point data sets relative to scattered point data sets, though this approach would not itself answer the question of which data collection strategy is best.

# Compare performance of scattered point regression with slope estimation.

# See whether one algorithm does better with certain size data sets.

# Compare difference in performance on 100,000 samples of four sizes:
# 10, 100, 1000, 10000.
sample.sizes = c(10, 100, 1000, 10000);
classical = c();
dual.point = c();

for (i in 1:length(sample.sizes))
{
  slopes = c();
  alt.slopes = c();

  errors = c();
  alt.errors = c();

  # Classical regression.
  for (iteration in 1:100000)
  {
    x = 1:sample.sizes[i];
    y = 2 * x + rnorm(sample.sizes[i]);
    slopes[iteration] = coef(lm(y ~ x))[2];
    errors[iteration] = abs(slopes[iteration] - 2);
  }

  # Dual point slope estimatation.
  for (iteration in 1:100000)
  {
    x = c(rep(1, sample.sizes[i] / 2), rep(sample.sizes[i], sample.sizes[i] / 2));
    y = 2 * x + rnorm(sample.sizes[i]);
    alt.slopes[iteration] = (mean(y[(sample.sizes[i] / 2 + 1):sample.sizes[i]]) - mean(y[1:(sample.sizes[i] / 2)])) / (sample.sizes[i] - 1);
    alt.errors[iteration] = abs(alt.slopes[iteration] - 2);
  }

  classical[i] = mean(errors);
  dual.point[i] = mean(alt.errors);
}