Doing Maximum Likelihood Estimation by Hand in R
Lately I’ve been writing maximum likelihood estimation code by hand for some economic models that I’m working with. It’s actually a fairly simple task, so I thought that I would write up the basic approach in case there are readers who haven’t built a generic estimation system before.
First, let’s start with a toy example for which there is a closed-form analytic solution. We’ll ignore that solution and use optimization functions to do the estimation. Starting with this toy example makes it easy to see how well an approximation system can be expected to perform under the best circumstances – and also where it goes wrong if you make poor programming decisions.
Suppose that you’ve got a sequence of values from an unknown Bernoulli variable like so:
p.parameter <- 0.8
sequence <- rbinom(10, 1, p.parameter)
# [1] 0 1 1 1 1 1 1 0 1 0
Given the sequence, we want to estimate the value of the parameter, p, which is not known to us. The maximum likelihood approach says that we should select the parameter that makes the data most probable. For a Bernoulli variable, this is simply a search through the space of values for p (i.e [0, 1]) that makes the data most probable to have observed.
It’s worth pointing out that the analytic solution to the maximum likelihood estimation problem is to use the sample mean. We’ll therefore use mean(sequence) as a measure of the accuracy of our approximation algorithm.
How do we find the parameter numerically? First, we want to define a function that specifies the probability of our entire data set. We assume that each observation in the data is independently and identically distributed, so that the probability of the sequence is the product of the probabilities of each value. For the Bernoulli variables, this becomes the following function:
likelihood <- function(sequence, p.parameter) {
likelihood <- 1
for (i in 1:length(sequence)) {
if (sequence[i] == 1) {
likelihood <- likelihood * p.parameter
}
else {
likelihood <- likelihood * (1 - p.parameter)
}
}
return(likelihood)
}
To do maximum likelihood estimation, we therefore only need to use an optimization function to maximize this function. A quick examination of the likelihood function as a function of p makes it clear that any decent optimization algorithm should be able to find the maximum:
possible.p <- seq(0, 1, by = 0.001)
jpeg('Likelihood_Concavity.jpg')
library('ggplot2')
qplot(
possible.p,
sapply(possible.p, function (p) {likelihood(sequence, p)}),
geom = 'line',
main = 'Likelihood as a Function of P',
xlab = 'P',
ylab = 'Likelihood'
)
dev.off()
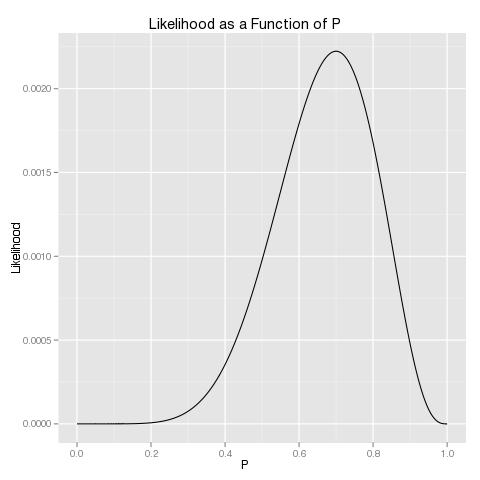
For single variable cases, I find that it’s easiest to use R’s base function optimize to solve the optimization problem:
mle.results <- optimize(
function(p) {likelihood(sequence, p)},
interval = c(0, 1),
maximum = TRUE
)
mle.results
# $maximum
# [1] 0.6999843
#
# $objective
# [1] 0.002223566
Here I’ve used an anonymous function that returns the likelihood of our current data given a value of p; I’ve also specified that the values of p must lie in the interval [0, 1] and asked optimize to maximize the result, rather than minimize, which is the default behavior. Examining the output of optimize, we can see that the likelihood of the data set was maximized very near 0.7, the sample mean. This suggests that the optimization approximation can work. It’s worth noting that the objective value is the likelihood of the data set for the specified value of p. The smallness of the objective for large problems can become a major problem. To understand why, it’s worth seeing what happens as the size of the sample grows from 10 to 2500 samples:
error.behavior <- data.frame()
for (n in 10:2500) {
sequence <- rbinom(n, 1, p.parameter)
likelihood.results <- optimize(
function(p) {likelihood(sequence, p)},
interval = c(, 1),
maximum = TRUE
)
true.mle <- mean(sequence)
likelihood.error <- true.mle - likelihood.results$maximum
error.behavior <- rbind(
error.behavior,
data.frame(
N = n,
Error = likelihood.error,
Algorithm = 'Likelihood'
)
)
}
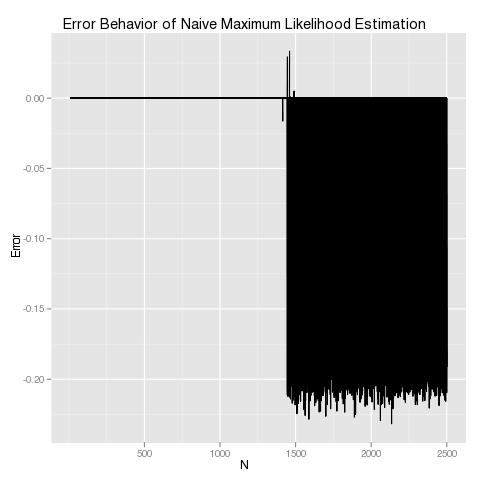
As you can see, our approximation approach works great until our data set grows, and then it falls apart. This is exactly the opposite of what asymptotical statistical theory tells us should be happening, so it’s clear that something is going very wrong. A quick examination of the results from the last pass through our loop makes clear what’s wrong:
sequence <- rbinom(2500, 1, p.parameter)
likelihood.results <- optimize(
function(p) {likelihood(sequence, p)},
interval = c(, 1),
maximum = TRUE
)
likelihood.results
# $maximum
# [1] 0.9999339
#
# $objective
# [1] 0
The likelihood of our data is numerically indistinguishable from 0 given the precision of my machine’s floating point values. Multiplying thousands of probabilities together is simply not a viable approach without infinite precision. Thankfully, there’s a very simple solution: replace all of the probabilities with their logarithms. Instead of maximizing the likelihood, we maximize the log likelihood, which involves summing rather than multiplying, and therefore stays numerically stable:
log.likelihood <- function(sequence, p) {
log.likelihood <- 0
for (i in 1:length(sequence)) {
if (sequence[i] == 1) {
log.likelihood <- log.likelihood + log(p)
} else {
log.likelihood <- log.likelihood + log(1 - p)
}
}
return(log.likelihood)
}
You can check that this problem is as easily solved numerically as the original problem by graphing the log likelihood:
sequence <- c(0, 1, 1, 1, 1, 1, 1, 0, 1, 0)
possible.p <- seq(0, 1, by = 0.001)
jpeg('Log_Likelihood_Concavity.jpg')
qplot(
possible.p,
sapply(possible.p, function (p) {log.likelihood(sequence, p)}),
geom = 'line',
main = 'Log Likelihood as a Function of P',
xlab = 'P',
ylab = 'Log Likelihood'
)
dev.off()
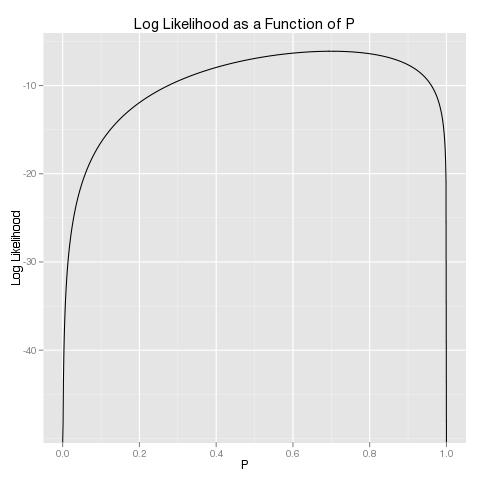
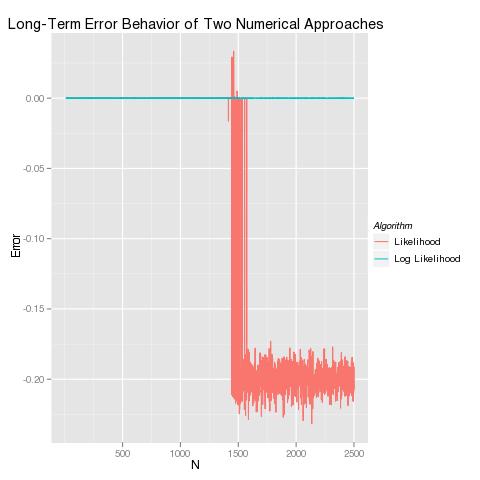
And then you can rerun our error diagnostics using both approaches to confirm that the log likelihood approach does not suffer from the same numerical problems:
error.behavior <- data.frame()
for (n in 10:2500) {
sequence <- rbinom(n, 1, p.parameter)
likelihood.results <- optimize(
function(p) {likelihood(sequence, p)},
interval = c(0, 1),
maximum = TRUE
)
log.likelihood.results <- optimize(
function(p) {log.likelihood(sequence, p)},
interval = c(0, 1),
maximum = TRUE
)
true.mle <- mean(sequence)
likelihood.error <- true.mle - likelihood.results$maximum
log.likelihood.error <- true.mle - log.likelihood.results$maximum
error.behavior <- rbind(
error.behavior,
data.frame(
N = n,
Error = likelihood.error,
Algorithm = 'Likelihood'
),
data.frame(
N = n,
Error = log.likelihood.error,
Algorithm = 'Log Likelihood'
)
)
}
jpeg('Long-Term_Error_Behavior.jpg')
ggplot(
error.behavior,
aes(x = N, y = Error)
) +
geom_line(aes(group = Algorithm, color = Algorithm)) +
opts(
title = 'Long-Term Error Behavior of Two Numerical Approaches',
xlab = 'Sample Size',
ylab = 'Deviation from True MLE'
)
dev.off()
More generally, given any data set and any model, you can – at least in principle – solve the maximum likelihood estimation problem using numerical optimization algorithms. The general algorithm requires that you specify a more general log likelihood function analogous to the R-like pseudocode below:
log.likelihood <- function(
sequence.as.data.frame,
likelihood.function,
parameters
) {
log.likelihood <- 0
for (i in 1:nrow(sequence.as.data.frame)) {
log.likelihood <- log.likelihood +
log(likelihood.function(sequence.as.data.frame[i, ], parameters))
}
return(log.likelihood)
}
Then you need to apply multivariable, constrained optimization tools to find your maximum likelihood estimates. This actually turns out to be a hard problem in general, so I’m going to bail out on the topic here.