A 3D Version of R's curve() Function

I like exploring the behavior of functions of a single variable using the curve() function in R. One thing that seems to be missing from R’s base functions is a tool for exploring functions of two variables.

I asked for examples of such a function on Twitter today and didn’t get any answers, so I decided to build my own. As I see it, there are two ways to visualize a function of two variables:

1. Use a 3D surface.
2. Use a heatmap.

But 3D surfaces aren’t currently available in ggplot2, so I decided to work with heatmaps. The function below provides a very simple implementation of my 3D version of curve(), which I call curve3D():

curve3D <- function(f, from.x, to.x, from.y, to.y, n = 101) {
    x.seq <- seq(from.x, to.x, (to.x - from.x) / n)
    y.seq <- seq(from.y, to.y, (to.y - from.y) / n)
    eval.points <- expand.grid(x.seq, y.seq)
    names(eval.points) <- c('x', 'y')
    eval.points <- transform(
        eval.points,
        z = apply(
            eval.points,
            1,
            function (r) {f(r['x'], r['y'])}
        )
    )
    p <- ggplot(eval.points, aes(x = x, y = y, fill = z)) +
        geom_tile()
    print(p)
}

Here’s an example of the use of curve3D to explore the behavior of Loewenstein and Prelec’s Generalized Hyperbolic discounting function:

g <- function(x, y) {(1 + y * 2) ^ (-x / y) * (1 + y * 1) ^ (x / y)}

curve3D(g, from.x = 0.01, to.x = 1, from.y = 0.01, to.y = 1)

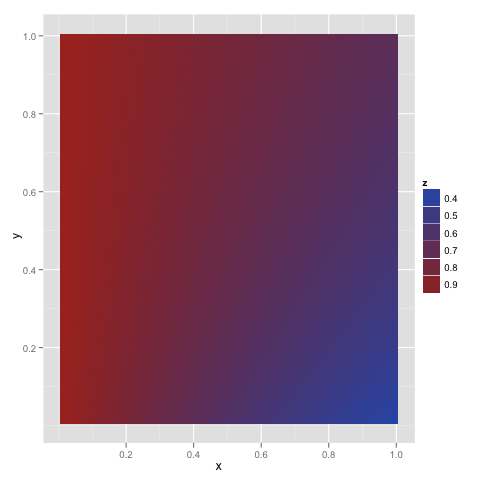
I’d love suggestions for cleaning this function up. Two obvious improvements are:

1. Allow the function to accept arbitrary expressions and not just functions as inputs.
2. Allow the user to see 3D surfaces or heatmaps.

I suspect that the first problem would be a great way to learn about functional programming in R – especially R’s methods for quoting, parsing and deparsing expressions.