Optimization Functions in Julia

Update 10/30/2013: Since this post was written, Julia has acquired a large body of optimization tools, which have been grouped under the heading of JuliaOpt.

Over the last few weeks, I’ve made a concerted effort to develop a basic suite of optimization algorithms for Julia so that Matlab programmers used to using fminunc() and R programmers used to using optim() can start to transition code over to Julia that requires access to simple optimization algorithms like L-BFGS and the Nelder-Mead method.

As of today, I believe that enough progress has been made to justify publicly announcing the first draft of an optimization suite for Julia tentatively called optim.jl. I intend to keep working on optim.jl for the next few months and expect that it will eventually become one of the first Julia packages.

For an end-user, interactions with optim.jl should take place almost entirely through the `optimize()` function, which I demonstrate how to use below in the context of minimizing the Rosenbrock function:

load("src/init.jl")

function rosenbrock(x::Vector)
    (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2
end

function rosenbrock_gradient(x::Vector)
    [
        -2.0 * (1.0 - x[1]) - 400.0 * (x[2] - x[1]^2) * x[1],
        200.0 * (x[2] - x[1]^2),
    ]
end

function rosenbrock_hessian(x::Vector)
    h = zeros(2, 2)
    h[1, 1] = 2.0 - 400.0 * x[2] + 1200.0 * x[1]^2
    h[1, 2] = -400.0 * x[1]
    h[2, 1] = -400.0 * x[1]
    h[2, 2] = 200.0
    h
end

problem = Dict()
problem[:f] = rosenbrock
problem[:g] = rosenbrock_gradient
problem[:h] = rosenbrock_hessian
problem[:initial_x] = [0.0, 0.0]
problem[:solution] = [1.0, 1.0]

algorithms = [
    "naive_gradient_descent",
    "gradient_descent",
    "newton",
    "bfgs",
    "l-bfgs",
    "nelder-mead",
    "sa",
]

for algorithm = algorithms
    results = optimize(
        problem[:f],
        problem[:g],
        problem[:h],
        problem[:initial_x],
        algorithm,
        10e-8,
        true,
    )
    print(results)
end

I think the code in my current draft of optim.jl is basically usable, but I’m still a little unsure of its correctness as I’ve never developed optimization algorithms before. I’ve set up a basic suite of benchmark functions to test these functions, but I could really use some additional use cases and benchmarks. If you’re interested, please submit pull requests through GitHub that provide new functions that you want optim.jl to be able to minimize automatically. If you submit a function, please provide the function itself, its gradient, its Hessian, a starting point and the global minimum of the function.

I’ve already set up five test functions as benchmarks, which are:

1. A simple exponential function.
2. A simple parabolic function.
3. A simple 4th-degree polynomial function.
4. The Rosenbrock function.
5. The Powell function.

The code for these five functions can be seen on GitHub along with drafts of a few other functions.

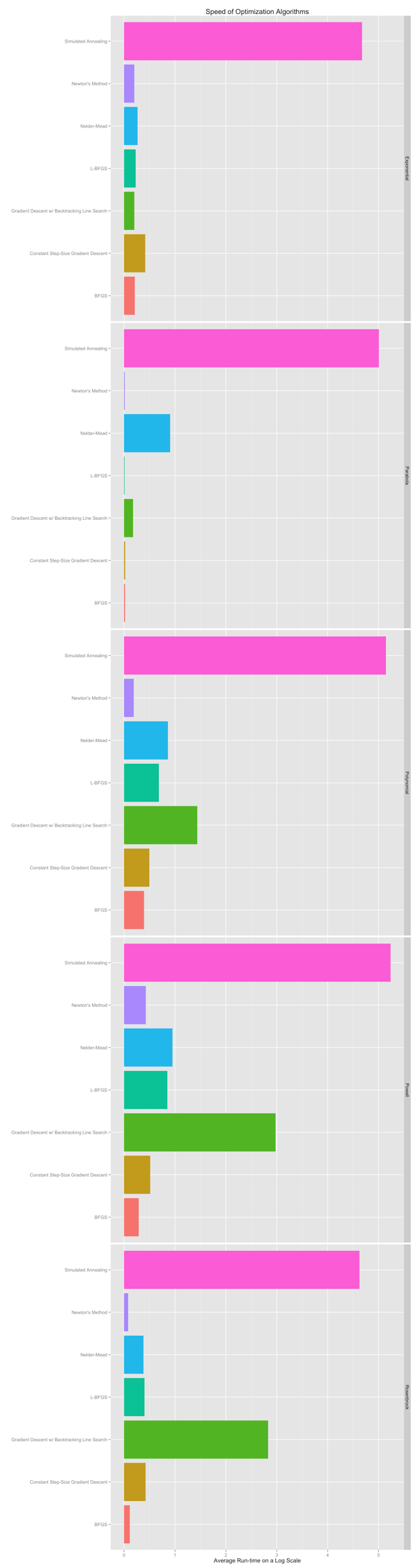
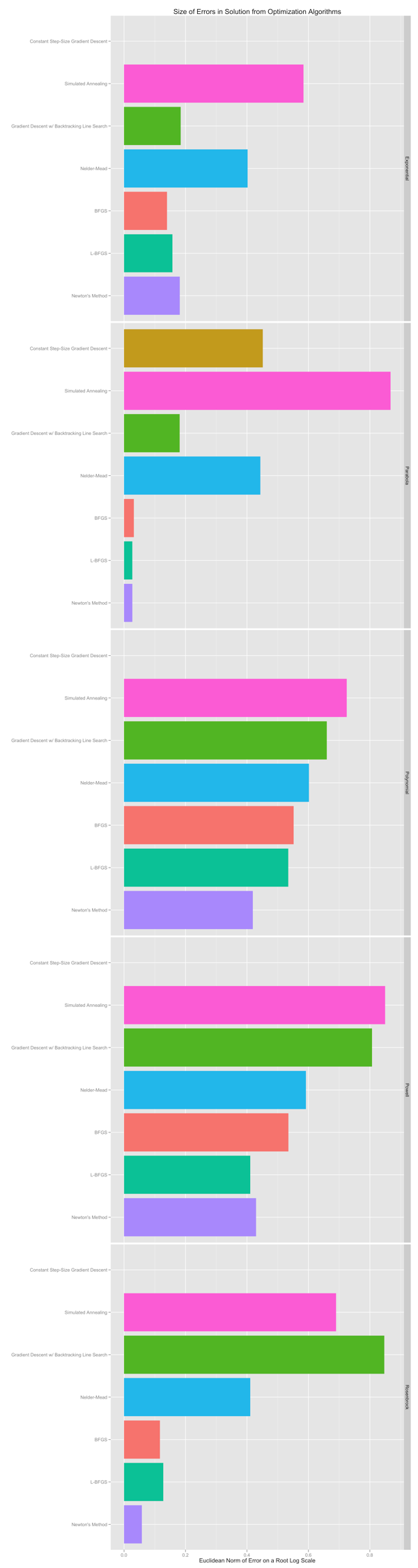
Below you can see plots that depict the performance of the seven algorithms that are currently available on each of these five problems. In some of these plots the bar for Naive Gradient Descent drops out: that’s because the constant step-size gradient descent algorithm behaves pathologically and produces NaN’s at some point. I’d stay away from that function unless you’re sure it’s what you want.

Stepping away from the perils of hard-coding a step-size for gradient descent, I think the take away message from these plots is that you should use BFGS, L-BFGS or Newton’s Method if you can compute or safely approximate the Hessian of a function. Only fall back on the other four methods if you find that you really need to avoid using even approximate Hessians or can’t compute the gradient of your to-be-minimized function.

The next few steps ahead are to add a few more optimization methods including Brent’s method and conjugate gradients; then start working on constrained optimization; and finally get to work on incorporating automatic differentiation and finite differencing. With those things in place, I think we’ll have a basic optimization function for Julia that will let us keep up with R’s optim. I think we’ve got a long way to go to catch up with fminunc, but I’m sure we’ll get there by the time Julia hits a 1.0 release.