Overfitting

What do you think when you see a model like the one below?

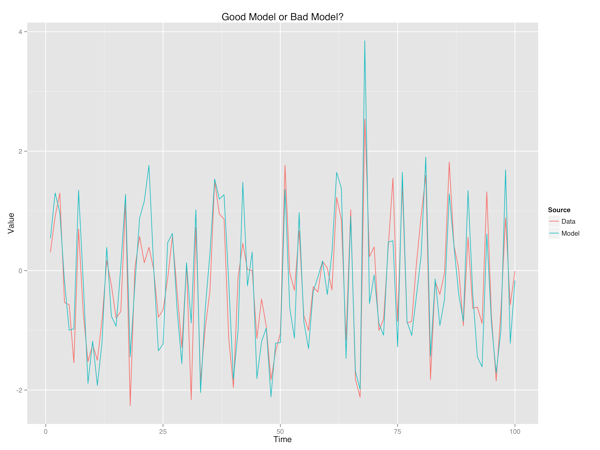
Does this strike you as a good model? Or as a bad model?

There’s no right or wrong answer to this question, but I’d like to argue that models that are able to match white noise are typically bad things, especially when you don’t have a clear cross-validation paradigm that will allow you to demonstrate that your model’s ability to match complex data isn’t a form of overfitting.

There are many objective reasons to suspect complicated models, but I’d like to offer up a subjective one. A model that fits complex data as perfectly as the model above is likely to not be an interpretable model1 because it is essentially a noisy copy of the data. If the model looks so much like the data, why construct a model at all? Why not just use the raw data?

Unless the functional form of a model and its dependence on inputs is simple, I’m very suspicious of any statistical method that produces outputs like those shown above. If you want a model to do more than produce black-box predictions, it should probably provide predictions that are relatively smooth. At the least it should reveal comprehensible and memorable patterns that are non-smooth. While there are fields in which neither of these goals is possible (and others where it’s not desirable), I think the default reaction to a model fit like the one above should be: “why does the model make such complex predictions? Isn’t that a mistake? How many degrees of freedom does it have that it can so closely fit such noisy data?”