The Shape of Floating Point Random Numbers
[Updated 10/18/2012: Fixed a typo in which mantissa was replaced with exponent.]
Over the weekend, Viral Shah updated Julia’s implementation of randn() to give a 20% speed boost. Because we all wanted to test that this speed-up had not come at the expense of the validity of Julia’s RNG system, I spent some time this weekend trying to get tests up and running. I didn’t get far, but thankfully others chimed in and got things done.
Testing an RNG is serious business. In total, we’ve considered using four different test suites:
All of these suites can be easily used to test uniform random numbers over unsigned integers. Some are also appropriate for testing uniform random numbers over floatint-point values.
But we wanted to test a Gaussian RNG. To do that, we followed Thomas et al.’s lead and mapped the Gaussian RNG’s output through a high-precision quantile function to produce uniform random floating point values. As our high-precision quantile function we ended up using the one described in Marsaglia’s 2004 JSS paper.
With that in place, I started to try modifying my previous RNG testing code. When we previously tried to test Julia’s rand() function, I got STS working on my machine and deciphered its manual well enough to run a suite of tests on a bit stream from Julia.
Unfortunately I made a fairly serious error in how I attempted to test Julia’s RNG. Because STS expects a stream of random 0’s and 1’s, I converted random numbers into 0’s and 1’s by testing whether the floating point numbers being generated were greater than 0.5 or less than 0.5. While this test is not completely wrong, it is very, very weak. Its substantive value comes from two points:
- It confirms that the median of the RNG is correctly positioned at 0.5.
- It confirms that the placement of successive entries relative to 0.5 is effectively random. In short, there is not trivial correlation between successive values.
Unfortunately that’s about all you learn from this method. We needed something more. So I started exploring how to convert a floating point into bits. Others had the good sense to avoid this and pushed us forward by using the TestU01 suite.
I instead got lost exploring the surprising complexity of trying to work with the individual bits of random floating point numbers. The topic is so subtle because the distribution of bits in a randomly generated floating point number is extremely far from a random source of individual bits.
For example, a uniform variable’s representation in floating point has all the following non-random properties:
- The sign bit is never random because uniform variables are never negative.
- The exponent is not random either because uniform variables are strictly contained in the interval [0, 1].
- Even the mantissa isn’t random. Because floating point numbers aren’t evenly spaced in the reals, the mantissa has to have complex patterns in it to simulate the equal-spacing of uniform numbers.
Inspired by all of this, I decided to get a sense for the bit pattern signature of different RNG’s. Below I’ve plotted the patterns for uniform, normal, gamma and Cauchy variables using lines that describe the mean value of the i-th bit in the bit string. At a minimum, a completely random bit stream would have a flat horizontal line through 0.5, which many of the lines touch for a moment, but never perfectly match.
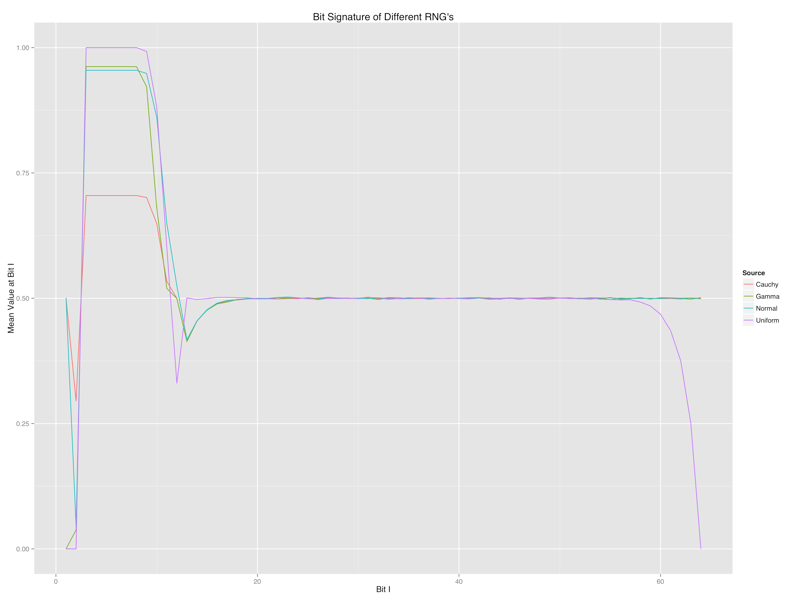
Some patterns:
- The first bit (shown on the far left) is the sign bit: you can clearly see which distributions are symmetric by looking for a mean value of 0.5 versus those that are strictly positive and have a mean value of 0.0.
- The next eleven bits are the exponent and you can clearly see which distributions are largely concentrated in the interval [-1, 1] and which have substantial density outside of that region. This bit would clue you into the variance of the distribution.
- You can see that there is a lot of non-randomness in the last few bits of the mantissa for uniform variables. There’s also non-randomness in the first few bits for all variables. I don’t yet have any real intuition for those patterns.
You can go beyond looking at the signatures of mean bit patterns by looking at covariance matrices as well. Below I show these covariances matrices in a white-blue coloring scheme in which white indicates negative values, light blue indicates zero and dark blue indicates positive values. Note that matrices, generated using R’s image() function are reflections of the more intuitive matrix ordering in which the [1,1] entry of the matrix occurs in the top-left instead of the bottom-left.
Uniform Variables
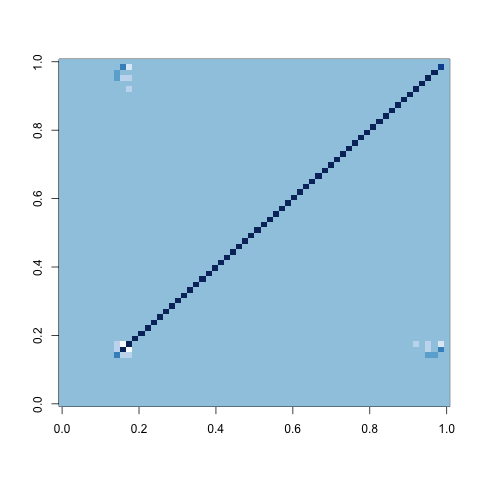
Normal Variables
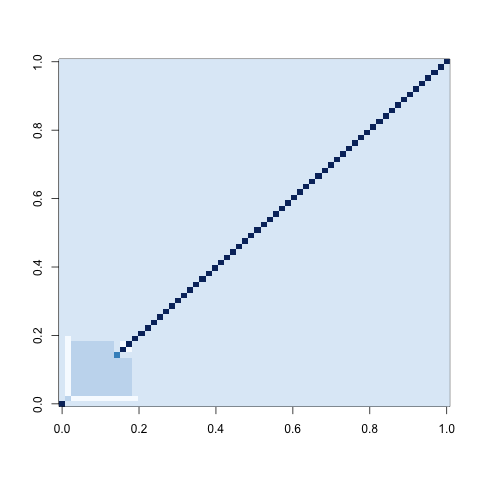
Gamma Variables
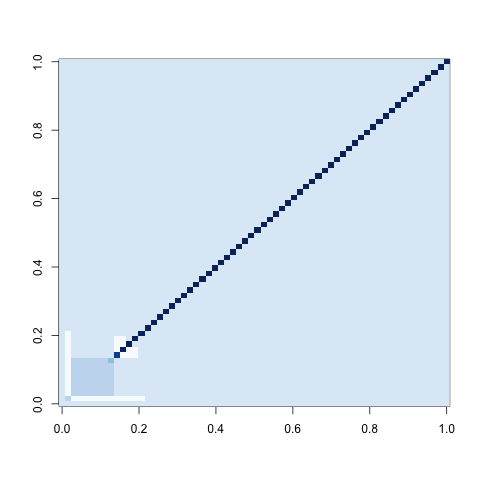
Cauchy Variables
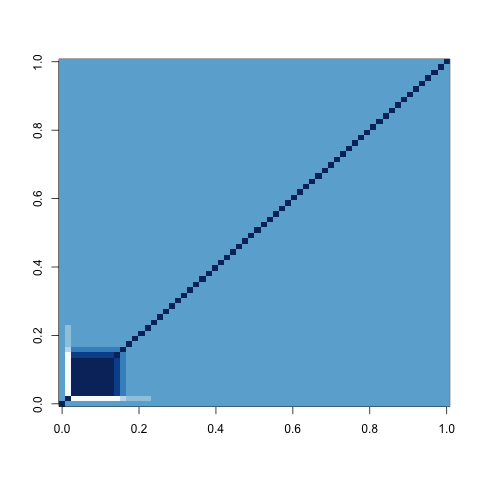
I find these pictures really helpful for reminding me how strangely floating point numbers behave. The complexity of these images is so far removed from the simplicity of the bit non-patterns in randomly generated unsigned integers, which can be generated using IID random bits and concatenating them together.