Introduction

In the third installment of my series of criticisms of NHST, I focused on the notion that a p-value is nothing more than a one-dimensional representation of a two-dimensional space in which (1) the measured size of an effect and (2) the precision of this measurement have been combined in such a way that we can never pull those two dimensions apart again. Because the size of a p-value depends on two fully independent factors, measured p-values will become smaller when either (A) a researcher focuses on studying an effect whose true magnitude is greater or (B) a researcher works harder to increase the precision of the measurement of the effect they are already committed to studying.

I’d like to dwell on this second strategy for producing low p-values for a moment, because I believe it suggests that p-values – in the hands of a social scientist committed to studying effects that are never exactly zero nor likely to be large in magnitude – are simply a confusing way of reporting the precision of our measurements. Moreover, because the precision of our measurements can always be increased by gathering more data or acquiring better equipment, p-values in the social sciences are nothing more than measures of the effort and money we invest in acquiring more precise measurements, even though many of us would like to think of p-values as a measure of the truth of our hypotheses.

To hammer home the notion that p-values are, in practice, just measurements of sample size, I’m going to provide the reader with a simple algorithm that any researcher can use to insure that essentially any study in the social sciences will, in expectation, be validated as true by the NHST approach to assessing research. For the sake of argument, we’ll insist that our hypothetical study should pass the classical threshold of p < .05.

At a high level, the approach I’ll take is similar in spirit to power analysis, but it is different in the details. In power analysis, you would tell me (1) the size of the effect you expect and (2) the sample size you can expect to gather; I would then hand you back the probability of successfully passing the p-value threshold you’ve set. In the approach described here, you hand me only the size of the expected effect; I then hand you back the minimum sample size you need to gather so that, in expectation, you’ll pass the p < .05 threshold. In other words, for any hypothesis you could possibly invent that isn’t absolutely false, you can take the information I’ll give you and run an experiment with the expectation that you will be able to use NHST to support your hypothesis. This experiment may be extremely expensive to run and may contribute nothing to human welfare if completed successfully, but you can run the experiment in reasonable confidence that you’ll be able to publish your results.

To do this, we only need to turn a simple calculation over to our computer:

1. For any proposed effect size, epsilon, we generate many different random samples of N normally distributed data points centered at epsilon.
2. For each sample, we run a one-sample t-test comparing the mean of that sample against 0. We store a copy of the p-value associated with this t-test.
3. Across samples, we average the p-values derived from these t-tests to estimate the expected p-value for a fixed sample size.
4. If the expected p-value is greater than .05, we increase N to N + 1 and try again.
5. Eventually we will find a large enough value of N so that the expected p-value is below .05: we store this in a database and move on to the next effect size.

If we generate a large enough number for different data sets for each of our effect sizes, our Monte Carlo estimates of the expected p-values will hopefully be accurate. With a large number for these estimates for different effect sizes, we can extrapolate out a smooth curve that shows the minimum sample size required to have an expectation that the p-value for a study with that sample size and effect size will be less than .05.

To calculate these values, I’ve coded up this simple search algorithm in R and put the code up on GitHub. In this post, I’ll simply provide a graph that shows how large a value of N is required to expect to pass a standard t-test as the size of the effect you’re studying grows along a logarithmic scale starting at 0.1 and going all the way up to 10:

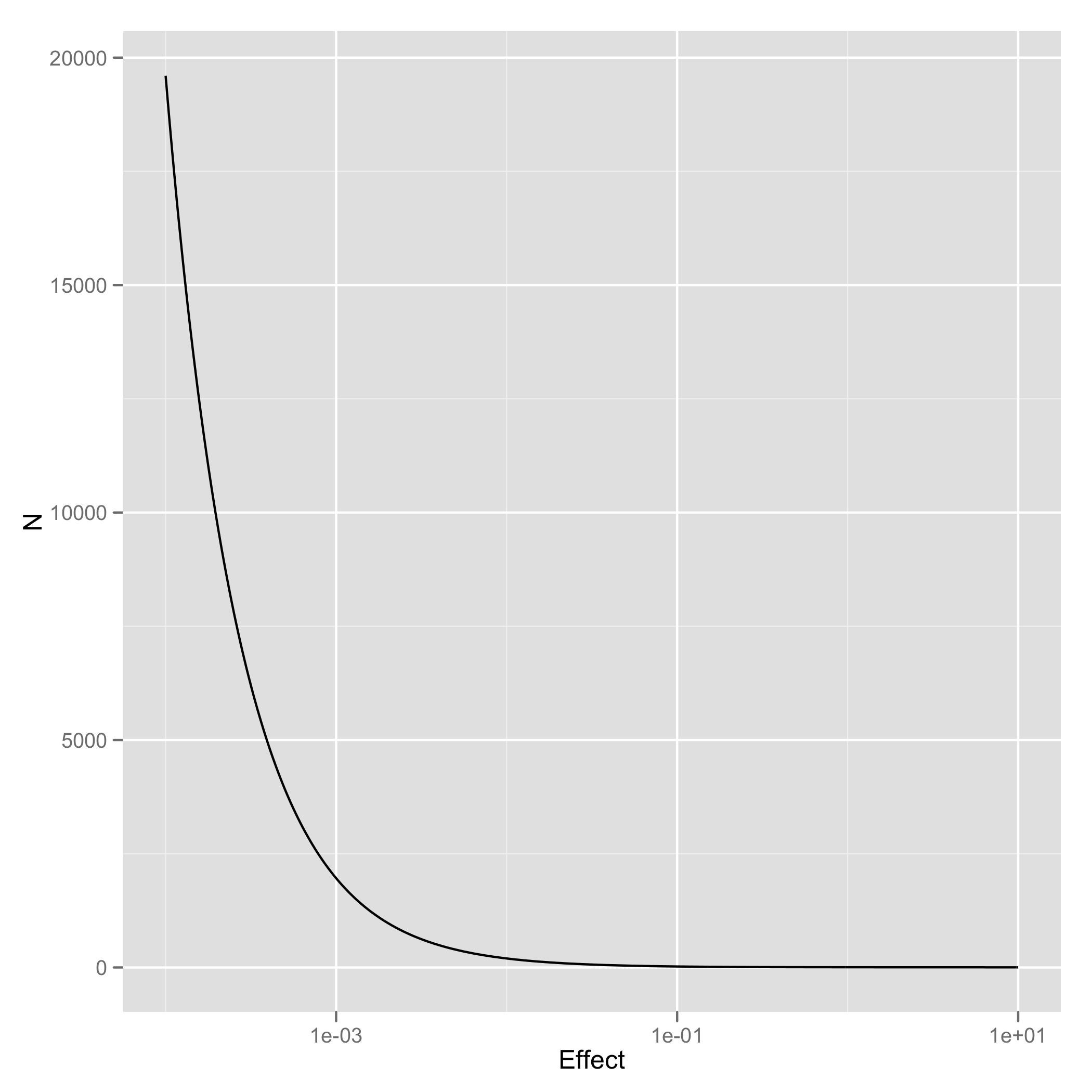
As you can see, you need huge sample sizes for effects as small as 0.1, but you can use remarkably few data points when the effect is sufficiently large. No matter how small your effect may be, you can always do the hard work of gathering data in order to pass the threshold of p < .05. As long as the effect you’re studying isn’t non-existent, p-values just measure how much effort you’ve put into collecting data.

Conclusions

What should we take away from this? A variety of conclusions could be drawn from thinking about the graph above, but I’m really only concerned with one of them: if your field always studies effects that aren’t exactly zero, it is always possible to design a study that can be expected to pass a significance test. As such, a significance test cannot, in principle, allow science to filter out any idea in the social sciences, except perhaps for those so outlandish that they do not have even a shred of truth in them. All that NHST does is measure how precise your measurement system is – which in turn is nothing more than a metric of how hard you were willing to work to gather data in support of your hypothesis. But the width of a confidence interval is clearly a superior tool for measuring the precision of your measurements, because it directly tells you the precision of your measurements; a p-value only tells you the precision of a measurement after you’ve pealed off the residue left behind by the size of the effect you’re studying.

Thankfully, I think that there are many viable approaches for presenting scientific research and evaluating the research of others that are far superior to p-values. In the next and final post in this series, I’ll focus on some suggestions for developing better strategies for analyzing data in the social sciences. Unfortunately, these better strategies require more than a change in methods in the social sciences, they require a change in culture. We need to do less hypothesis testing and more estimation of formal models. But I’ll leave the details of that until my next post.

[P.S. Many thanks to Sean Taylor for useful feedback on a draft of this post.]