Introduction

Neil Kodner recently got me interested again in analyzing Canabalt scores statistically by writing a great post in which he compared the average scores across iOS devices. Thankfully, Neil’s made his code and data freely available, so I’ve been revising my original analyses using his new data whenever I can find a free minute.

Returning to Canabalt has been a lot of fun, especially because my grasp of statistical theory is a lot stronger now than it was when I published my last post on Canabalt scores. For example, I actually know now what I was trying to say when I publicly described my search for a Poisson distribution in the posted scores. At the time, I had just read about Poisson regressions and was therefore eager to fit Poisson models to the scores data, even though the Poisson model gave very poor results. In retrospect, it’s clear that I was misled by superficial similarities in statistical terminology. What I was really looking for in the data was something closer to a Poisson process than to a Poisson distribution. Unfortunately, I didn’t really understand Poisson processes at the time I wrote my original posts, so I only succeeded in showing that Canabalt scores could not reasonably be claimed to be Poisson distributed.

Generating Process

But now that I have more data and more experience, it’s easy to see what I was struggling to articulate before: Canabalt scores seem to be generated by something like a truncated Poisson process. From my current perspective, the generating process for a Canabalt score is essentially the following:

1. Initialize the player’s score to zero.
2. Iterate the following steps repeatedly:
3. Draw the number of meters before the next obstacle from a Poisson distribution. Add this value to the player’s current score.
4. Draw the identity of the next obstacle from a multinomial distribution.
5. For every type of obstacle, there is a constant probability p that a player will die when they come up against an instance of that type of obstacle. Given the value of p, draw a Bernoulli variable with probability p of coming up heads. If the result is heads, the player dies and their score is the current value of score, which is therefore simply the sum of several Poisson variables. If the result is tails, go back to the top of this loop.

This intuition, unfortunately, isn’t trivial to express as a model that I can quickly fit to the data I have. I haven’t tried very systematically to build a formal version of this model because there seem to be obvious problems of identification. For example, one can imagine that the values for the obstacle-specific probabilities described above can all be lowered by a constant proportion at the same time that the mean of the underlying Poisson distribution is decreased while the distribution of outcome scores is left constant. My intuition tells me that the only way around this would be to exploit the variance of the data and the restriction of the Poisson distribution to integer values, but I haven’t pushed very hard on this. If others are interested in pursuing it, I think there’s an interesting open problem here.

Thankfully, there’s another approach to modeling the data that’s simpler. As Owe Jessen noted in a comment on my earlier post, the distribution of scores looks like one parameterization of the gamma distribution. When Owe made this suggestion originally, I tried to use fitdistr from the MASS package to fit a gamma model to the scores data, but was never able to get the code to work properly. But now that I’m reasonably fluent in BUGS, it’s quite easy to fit a gamma distribution to the empirical scores data.

Gamma Distribution

Using JAGS, fitting a gamma distribution to the scores data is basically a trivial problem that requires only a few lines of code:

model {
    for (i in 1:N) {
        score[i] ~ dgamma(shape, rate)
    }

    shape ~ dgamma(0.0001, 0.0001)
    rate ~ dgamma(0.0001, 0.0001)
}

Invoking this BUGS model from R using code that I’ve put on GitHub allows us to estimate the scale and rate parameters for a gamma distribution in a few minutes. The resulting parameterization of the gamma distribution looks very similar to the empirical density that we can estimate using a KDE:

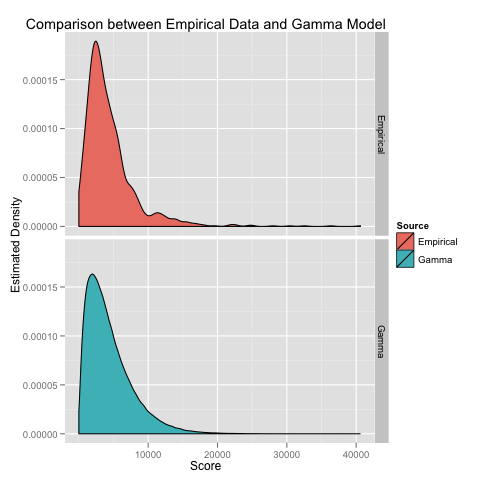
Beyond visual comparisons, we can formally test the fit of the gamma model using a K/S test. The K/S test tells us that we should reject the gamma model, but it’s a fairly weak rejection at p = 0.005. Given that we have over a thousand data points, I think this weak rejection suggests that the gamma model is not such a bad approximation to the true score distribution.

Where the gamma model seems to noticeably fail is in the tail of the scores distribution:

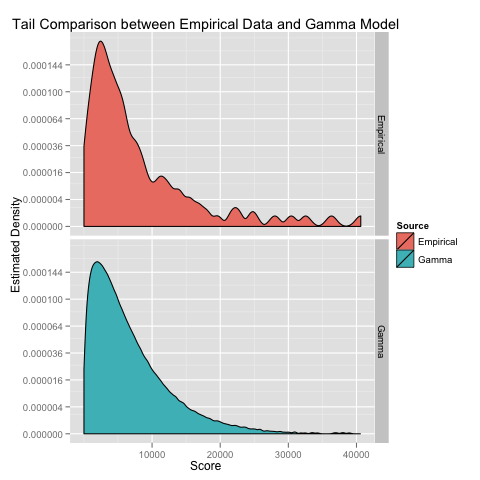
To exaggerate the differences here, I’ve used a square root transform on the y axis so that we can see the bumps in the estimated density plot that are missing from the theoretical gamma model.

Since generating these images, I’ve had a chance to read a bit about heavy tailed distributions, but haven’t yet tried fitting any of them to this data set. I’ll probably start with a Pareto distribution, though I’d really like to find a discrete heavy tailed distribution over the natural numbers rather than a continuous distribution over the non-negative reals.

Looking further past the gamma model’s misfit in the tails, there’s another reason that I like the gamma model: the gamma distribution has an origins story that has some points of connection to the generative model I outlined above. Specifically, adding a bunch of exponential variables together will give you a gamma distribution (also called an Erlang distribution in this context). While I’m skeptical that the distribution of meters between obstacles can be reasonably treated as if it were an exponential distribution, the summation origin for the gamma distribution is a nice point of connection to my intuitions about a data generating mechanism that behaves like a Poisson process.

Hierarchical Gamma Model

The gamma model has another point in its favor: it’s easy to write down a hierarchical model that fits a distinct gamma distribution to subsets of the original data. By fitting multiple gamma distributions, we can easily make comparisons between the estimated score distributions for the different devices that Neil analyzed. As Neil showed, there are enough rows in the current data to do this in a principled way across devices without resorting to gamma distributions, but a hierarchical model provides us with tools for thinking about comparisons across different types of deaths, where we don’t have enough data to use density estimates or other non-parametric methods.

Without a distributional model, I’d be skeptical about estimating differences between groups with such unequal sample sizes. (Even with a model, I don’t think we can make strong conclusions about differences between all of the groups in this data set.) That said, within a hierarchical model, I feel more comfortable estimating several conditional distributions from a small data set, because the hierarchical model provides enough shrinkage to prevent us from arriving at extreme conclusions simply because some groups were undersampled in our data set. (Of course, shrinking the model parameters for small groups towards the global mean may lead us to miss differences that are real.)

All that said, the analyses I describe below implement a hierarchical model that I’ve used to estimate the mean and standard deviation of the score distribution for each of the iOS devices and each of the death types in our data set.

First, let’s model the expected score for a player who died because of each of the various possible obstacles they might come across. I’ll refer to these different types of deaths as the death types. My JAGS code for estimating the shape and rate parameters for each death type is below:

model {
    for (i in 1:N) {
        score[i] ~ dgamma(shape[death[i]], rate[death[i]])
    }

    for (j in 1:K) {
        shape[j] ~ dgamma(alpha.shape, beta.shape)
        rate[j] ~ dgamma(alpha.rate, beta.rate)
    }

    alpha.shape ~ dgamma(0.0001, 0.0001)
    beta.shape ~ dgamma(0.0001, 0.0001)

    alpha.rate ~ dgamma(0.0001, 0.0001)
    beta.rate ~ dgamma(0.0001, 0.0001)
}

As you can see, I estimate group hyperparameters that partially pool data across all of the death types: these hyperparameters are themselves given weakly informative gamma priors in the last four lines of the model. The results give us the following estimates for the mean score for each death type along with the estimated standard deviation:

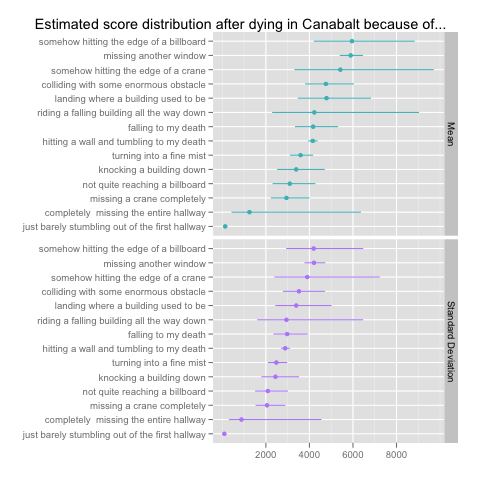
I’ve chosen to use means and standard deviations rather than the shape and rate parameters that we’re actually fitting, because the shape and rate parameters are on such different scales that only one of them can be visualized effectively at a time. There are simple formulas for translating between these parameterizations of the gamma distribution: the translation scheme can be found on Wikipedia.

Having estimated these parameters across death types, I can also approach the question that Neil addressed in his post by comparing the score distributions across iOS devices. The JAGS code to do so is almost identical to the code for estimating the gamma parameters across death types:

model {
    for (i in 1:N) {
        score[i] ~ dgamma(shape[device[i]], rate[device[i]])
    }

    for (j in 1:J) {
        shape[j] ~ dgamma(alpha.shape, beta.shape)
        rate[j] ~ dgamma(alpha.rate, beta.rate)
    }

    alpha.shape ~ dgamma(0.0001, 0.0001)
    beta.shape ~ dgamma(0.0001, 0.0001)

    alpha.rate ~ dgamma(0.0001, 0.0001)
    beta.rate ~ dgamma(0.0001, 0.0001)
}

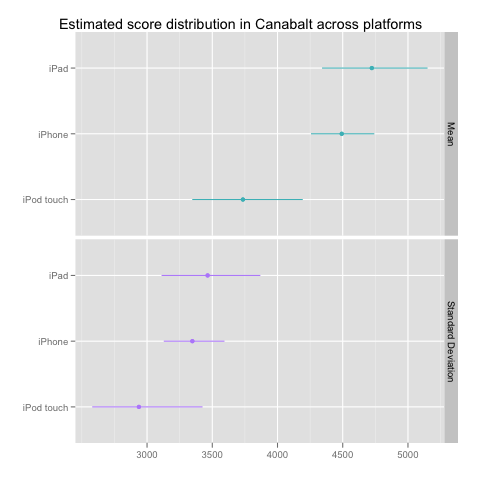
In this case, the results tell a much simpler story about the differences between the three devices in our data set:

Multinomial Model

As a closing point, there’s one more modeling project for which I’ve used JAGS on the new Canabalt data: I’ve tried to estimate the probability of suffering each type of death along with an indication of the uncertainty in our estimates. Of course, this is a simple problem to solve using maximum likelihood methods: you can just plug in the empirical frequencies. But, given my growing love for Bayesian methods and the use of credible intervals to summarize uncertainty, I decided that I would estimate the multinomial model for death types using a Dirichlet prior centered on a uniform multinomial distribution. Here’s my JAGS code for estimating the multinomial model:

model {
    deaths[1:K] ~ dmulti(p[1:K], N)
    p[1:K] ~ ddirch(alpha[1:K])

    for (i in 1:K) {
        alpha[i] <- 1 / K
    }
}

And here are the final results:

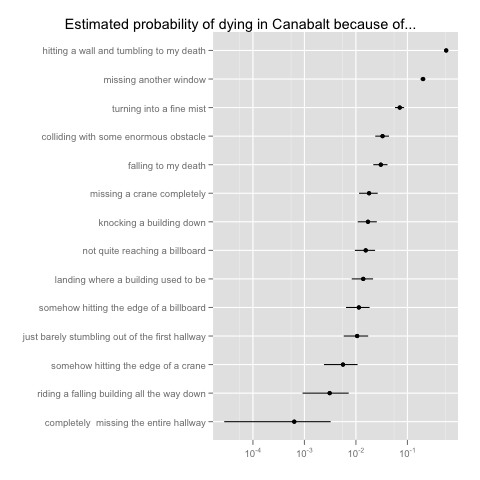
Conclusion

It’s been a lot of fun coming back to this topic. I still want to understand the outliers in the data better, but I’ll leave that for another day. If you’re interested in exploring this data set yourself, I encourage you to go to the GitHub repository I’ve set up and explore the JAGS code that I’ve used to fit these models. There you can also find higher effective resolution PDF’s of the graphs that you see here, which are admittedly a bit hard to read at this resolution.

Finally, I’d like to thank Neil Kodner for having put so much work into collecting more Canabalt data and analyzing it. Essentially all of the work I’ve done here is just a Bayesian reformulation of the questions that Neil addressed already in his own post.